“Connectivism leads to emergence.”
— Royal Institution, Mathematics Applied to AI (watch here)
I. Introduction: The Hidden Order of Connection
Artificial intelligence did not emerge from isolated genius or clever algorithms—it emerged from connection.
The Royal Institution’s lecture Mathematics Applied to AI captures this with precision: connectivism leads to emergence.
That phrase encapsulates one of the most important transitions in both natural and artificial systems—the moment when networked interactions among simple elements begin to produce complex, adaptive, and intelligent behavior.
It’s mathematics.
And it sits at the intersection of neural computation, complex systems theory, and cybernetic control—a framework deeply relevant to both AI engineering and modern security architectures.
II. Mathematical Foundations of Connectivism
At its core, connectivism is a mathematical model of learning defined by relationships, not rules.
Each connection between nodes represents a weighted influence—expressed through linear algebra, optimized through calculus, and probabilistically modulated through uncertainty.
-
Linear Algebra – Structure of Connection
Data is represented as vectors; relationships are encoded as matrices.- Matrix multiplication (
Wx) propagates influence through the network. - Eigenvectors describe stable attractors—directions of reinforced learning.
- Spectral topology defines how information diffuses across the system.
- Matrix multiplication (
-
Calculus – Dynamics of Change
Learning arises from gradient descent—the continuous optimization of a loss function across millions of interconnected parameters.- The chain rule translates local errors into global adjustments.
- Jacobian matrices describe the sensitivity of outputs to inputs—a core concept in adversarial robustness.
-
Probability and Information Theory – Managing Uncertainty
Every intelligent system must manage incomplete information.- Bayesian inference enables distributed reasoning under uncertainty.
- Entropy quantifies both surprise and information flow within the network.
- Mutual information measures how well signals across nodes cohere into understanding.
Mathematically, intelligence is not computed—it emerges through iterative optimization across an interconnected topology.
III. From Connectivism to Emergence
Emergence occurs when the density and interdependence of connections reach a threshold where collective behavior surpasses the capabilities of any individual node.
| Layer | Mathematical Domain | Observable Emergence |
|---|---|---|
| Neuronal | Nonlinear differential equations | Consciousness, pattern recognition |
| Algorithmic | Optimization & gradient flow | Language models, reasoning ability |
| Organizational | Network theory & control systems | Resilient cyber defense ecosystems |
| Societal | Game theory & information exchange | Innovation, instability, adaptation |
The common thread: interaction drives intelligence.
Once feedback loops close, the system begins to self-organize—discovering new behaviors not explicitly designed, but mathematically inevitable.
IV. HybridSec Implications: Networked Defense as a Living System
From a HybridSec perspective, “connectivism leads to emergence” describes not just AI systems but the evolution of modern cyber defense architectures.
Global threat detection networks increasingly resemble neural systems—distributed, adaptive, and self-correcting through feedback.
1. Distributed Cognition Across Sensors and Analysts
Telemetry streams, AI models, and human analysts form a hybrid cognitive mesh.
Each node specializes locally; global awareness emerges collectively.
2. Adaptive Feedback Loops
Machine learning pipelines and post-incident reviews act as synaptic reinforcement mechanisms.
Successful detections are strengthened; false positives are pruned. The network learns.
3. Information Flow as Lifeblood
Mathematically, cyber defense resilience correlates with connectivity entropy—too sparse and awareness decays; too dense and noise overwhelms.
Effective architectures balance signal-to-noise ratios across time and scale.
4. Phase Transitions in Intelligence Systems
As AI agents, analysts, and sensors become increasingly coupled, new emergent behaviors—both protective and unpredictable—begin to surface.
This demands an operational science of network phase management: keeping complexity adaptive without tipping into chaos.
V. The Future: Designing for Controlled Emergence
The next generation of AI and security systems will not be “programmed.”
They will be cultivated—grown within mathematically constrained environments where connectivity and feedback yield intelligence safely aligned to mission intent.
Research challenges ahead:
- Defining metrics of emergent intelligence across hybrid human–machine networks.
- Building interpretability frameworks rooted in information geometry, not just model inspection.
- Applying topological data analysis to visualize learning dynamics in real time.
- Exploring ethical containment models for self-organizing digital systems.
The discipline is moving from software engineering to system ecology—where intelligence is an emergent property of well-structured connectivity.
VI. Conclusion: The Geometry of Understanding
Connectivism leads to emergence.
That is the geometry of thought—whether in neurons, networks, or nations.
The mathematics behind intelligence is not a static equation but a living architecture.
Understanding it gives us the tools to build systems that can adapt, reason, and defend—not through command and control, but through connection and coherence.
🎥 Watch the source lecture:
Royal Institution – Mathematics Applied to AI
HybridSec Science — where intelligence and security converge.
Share this article

yankee0one
Scientific research analyst focused on the convergence of artificial intelligence, complex systems, and cyber defense.
Related Articles

Rules of Life: Simulating Evolution in a Shifting World
How resource scarcity, environmental change, and intra-species competition shape adaptive success—visualized through generative simulation.
Read more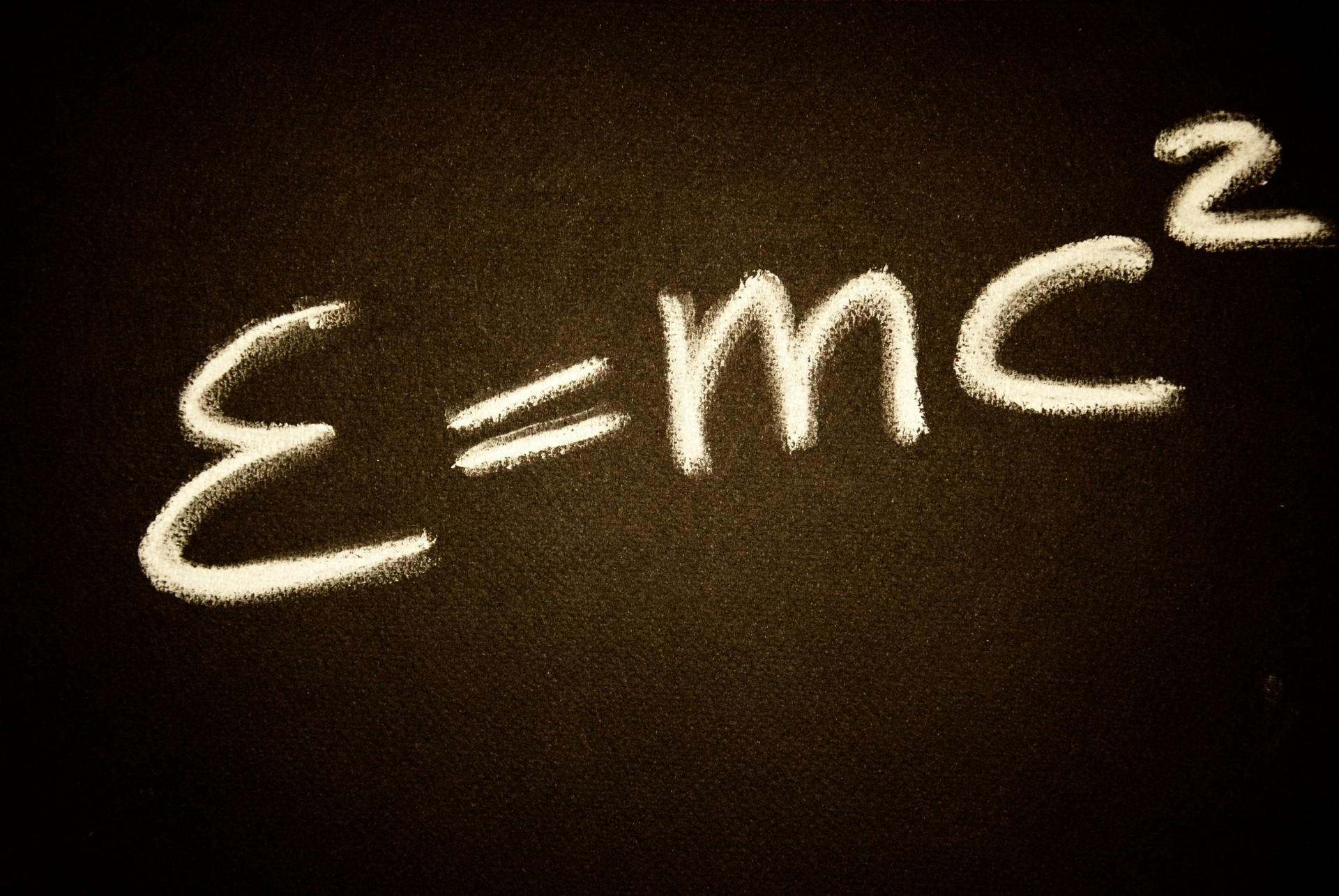
Quantum Computing in 2025: From Promise to Practicality
The quantum frontier is maturing rapidly in 2025, with real-world applications emerging in chemistry, logistics, cybersecurity, and AI integration.
Read more
Quantum Computing Breakthrough: A New Era in Scientific Research
Recent advances in quantum computing technology are setting the stage for revolutionary changes in scientific research methodologies across multiple disciplines.
Read more